1.1. Overview of the Problem
Understanding mathematical problems requires analyzing their structure and applying appropriate strategies. Resources like textbooks‚ online tutorials‚ and practice worksheets provide guidance for solving various math challenges effectively.
Mathematical problems often involve analyzing structures‚ applying strategies‚ and using resources like textbooks or online tutorials. These challenges require logical thinking and precise calculations. Resources such as practice worksheets and educational apps provide step-by-step guidance; Understanding the problem’s core is essential for applying the right mathematical concepts. This approach ensures effective problem-solving and fosters a deeper grasp of mathematical principles.
1.2. Importance of Solving the Problem
Solving mathematical problems enhances critical thinking and logical reasoning. It builds a strong foundation for understanding complex concepts in science‚ engineering‚ and everyday problem-solving. Accurate solutions validate theories and formulas‚ ensuring reliability in real-world applications. Mastery of math problems fosters academic success and prepares individuals for challenges requiring analytical skills. Regular practice strengthens mental agility and confidence in tackling diverse mathematical scenarios.

Types of Math Problems and Their Solutions
Math problems vary widely‚ encompassing algebra‚ calculus‚ geometry‚ and more. Recognizing problem types is crucial for applying appropriate strategies and solutions effectively.
2.1. Algebraic Problems
Algebraic problems involve solving equations and manipulating variables. They often require applying properties of equality‚ order of operations‚ and factoring. Common types include linear‚ quadratic‚ and polynomial equations. Properly isolating variables and avoiding arithmetic errors are crucial. Resources like textbooks and online tutorials provide step-by-step guidance for mastering algebraic techniques and strategies to solve complex equations effectively.
2.2. Calculus and Advanced Mathematics
Calculus and advanced math problems involve complex concepts like derivatives‚ integrals‚ and differential equations. These require precise application of mathematical principles and techniques. Resources such as textbooks and online tutorials provide detailed solutions and step-by-step guides. Practice with problems involving limits‚ series‚ and multivariable calculus helps build proficiency. Graphical tools and software also aid in visualizing and solving intricate mathematical models effectively.
2.3. Geometry and Trigonometry
Geometry and trigonometry involve solving problems related to shapes‚ angles‚ and spatial relationships. Common problems include finding lengths‚ areas‚ and volumes of geometric figures. Trigonometric identities and theorems‚ such as the Pythagorean theorem‚ are essential tools. Resources like textbooks and online tutorials provide step-by-step solutions for complex problems‚ while practice worksheets help reinforce understanding of concepts like triangles‚ circles‚ and vectors.
Step-by-Step Solution Guide
Start by understanding the problem statement‚ then break it down into manageable parts. Apply relevant mathematical concepts and verify each step to ensure accuracy and correctness.
3.1. Understanding the Problem Statement
Understanding the problem statement is the first crucial step in solving any mathematical problem. It involves identifying key elements‚ variables‚ and the relationships between them. Clarity in comprehension ensures that the approach taken is relevant and effective. Utilize resources like textbooks‚ online tutorials‚ and practice worksheets to refine your interpretation and grasp the core of the problem before proceeding to solve it systematically.
3.2. Breaking Down the Problem
Breaking down a math problem involves simplifying it into manageable parts. Identify key components‚ such as variables‚ constants‚ and relationships. Determine the unknowns and what needs to be solved. Use techniques like algebraic manipulation or geometric analysis to isolate elements. This structured approach ensures clarity and makes solving the problem more systematic. Utilize resources like textbooks or online tutorials for guidance on effective problem decomposition strategies.
3.3. Applying Relevant Mathematical Concepts
After breaking down the problem‚ apply appropriate mathematical concepts to each part. Use algebra for equations‚ geometry for spatial issues‚ or calculus for rates of change. Utilize truth tables for logical problems and graph theory for network issues. Practice with similar problems enhances concept application. Resources like textbooks and online tools aid in understanding and applying these concepts effectively.
3.4. Verifying the Solution
Verifying the solution ensures accuracy by cross-checking each step. Use truth tables for logical problems‚ reapply algebraic steps‚ or check graphical interpretations. Ensure all operations align with mathematical principles and that the final answer satisfies the original equation or condition. Consulting additional resources or peer reviews can further validate the solution’s correctness and completeness.
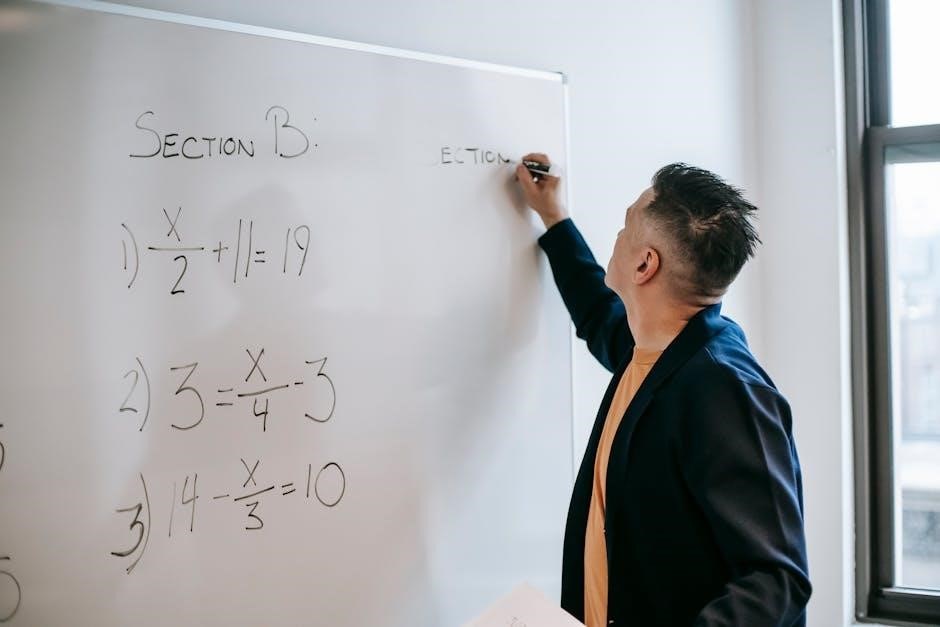
Common Mistakes and Misconceptions
Common errors include algebraic manipulation mistakes‚ misapplying theorems‚ and misinterpreting results. These oversights often stem from rushed problem-solving or inadequate understanding of foundational mathematical principles.
4.1. Errors in Algebraic Manipulations
Common algebraic errors include incorrect sign handling‚ improper distribution of terms‚ and miscalculations during arithmetic operations. These mistakes often arise from rushed problem-solving or a lack of attention to detail. Misapplying properties of equality or incorrectly simplifying expressions can lead to erroneous solutions. It is crucial to approach each step methodically and verify calculations to minimize such errors‚ ensuring the integrity of the mathematical process and its outcome.
4.2. Misapplication of Theorems and Formulas
One of the most prevalent errors in mathematical problem-solving is the misapplication of theorems and formulas. This often occurs when learners misunderstand the conditions under which a theorem or formula applies. For instance‚ using the quadratic formula for non-quadratic equations or applying the wrong trigonometric identity can lead to incorrect solutions. Additionally‚ neglecting to consider special cases or constraints can exacerbate these errors. It is essential to thoroughly understand the underlying principles and the appropriate contexts for applying mathematical tools to ensure accurate and valid results. Regular practice and review of foundational concepts can help mitigate such mistakes‚ fostering a deeper comprehension of mathematical theories and their practical applications. By grounding problem-solving in a solid understanding of when and how to apply specific theorems and formulas‚ individuals can enhance their mathematical proficiency and minimize errors.
4.3. Incorrect Interpretation of Results
Incorrectly interpreting mathematical results is a common mistake that can lead to flawed conclusions. This often happens when learners misread graphs‚ misapply statistical measures‚ or overlook critical assumptions. For example‚ confusing correlation with causation or misinterpreting the significance of a calculated value can result in erroneous decisions. It is crucial to critically evaluate results in their proper context and verify their alignment with the problem’s requirements. Regular practice in analyzing and presenting data can improve the accuracy of interpretations‚ ensuring that conclusions are both valid and meaningful. By fostering a habit of careful examination and reflection‚ individuals can avoid misunderstandings and enhance their problem-solving skills. Additionally‚ seeking feedback from peers or instructors can provide valuable insights and help refine one’s ability to interpret results correctly. This iterative process of learning and improvement is essential for mastering mathematical problem-solving and applying it effectively in real-world scenarios. As one becomes more proficient‚ the ability to discern and communicate accurate interpretations grows‚ leading to greater confidence and competence in tackling complex mathematical challenges.

Resources for Solving Math Problems
Textbooks‚ online tutorials‚ and practice worksheets are essential resources for solving math problems. They provide step-by-step guidance‚ examples‚ and exercises to enhance understanding and problem-solving skills.
5.1. Textbooks and Educational Materials
Textbooks like “Applied Mathematics” by J. David Logan and “The Red Book of Mathematical Problems” offer comprehensive coverage of various math topics. They provide step-by-step solutions‚ practice problems‚ and detailed explanations‚ catering to both elementary and advanced learners. These materials are invaluable for understanding concepts‚ mastering techniques‚ and preparing for exams. They often include real-world applications‚ making them essential for students seeking to enhance their problem-solving skills and mathematical knowledge.
5.2. Online Tutorials and Forums
Online platforms like Khan Academy‚ Coursera‚ and specialized math forums offer interactive lessons and community-driven solutions. Websites such as DeepMind and educational apps provide innovative tools for solving complex problems. These resources often include video tutorials‚ step-by-step guides‚ and discussion threads where users can ask questions and receive feedback. They cater to diverse learning styles and are accessible anytime‚ making them invaluable for students seeking additional support and real-time assistance.
5.3. Practice Worksheets and PDF Guides
Practice worksheets and PDF guides are invaluable for mastering mathematical concepts. Resources like NCERT solutions and CBSE sample papers offer structured exercises with answers. These guides cover algebra‚ calculus‚ and geometry‚ providing step-by-step solutions. They enable students to practice consistently‚ track progress‚ and reinforce learning. Many educational institutions and websites provide downloadable PDFs‚ ensuring access to high-quality practice materials tailored to various skill levels and curriculum requirements.
The Role of Technology in Solving Math Problems
Technology‚ such as AI tools and educational apps‚ revolutionizes math problem-solving by providing automated solutions‚ step-by-step guidance‚ and interactive learning experiences‚ enhancing both speed and accuracy.
6.1. Graphing Calculators and Software
Graphing calculators and software are powerful tools for visualizing and solving mathematical problems. They enable users to graph functions‚ explore relationships‚ and compute solutions for algebraic‚ calculus‚ and trigonometric problems. These tools often provide step-by-step solutions‚ making complex equations and concepts more accessible. They are particularly useful for students and professionals‚ offering interactive learning and real-time feedback to enhance understanding and problem-solving skills.
6.2. AI and Machine Learning Tools
AI and machine learning tools are revolutionizing math problem-solving by generating novel solutions and insights. Large language models (LLMs) like DeepMind’s system can tackle complex equations and provide step-by-step explanations. These tools enhance interactive learning‚ offering real-time feedback and aiding in understanding intricate mathematical concepts. They are particularly effective in solving algebraic‚ calculus‚ and advanced problems‚ making them invaluable for students and professionals seeking innovative solutions.
6.3. Educational Apps and Platforms
Educational apps and platforms like Khan Academy‚ Mathway‚ and Photomath offer interactive tools for solving math problems. These resources provide step-by-step solutions‚ video tutorials‚ and practice exercises. They cater to various skill levels‚ from basic algebra to advanced calculus. Many platforms also include community forums for discussion and personalized learning paths to enhance understanding and problem-solving skills in mathematics.
Real-World Applications of the Solution
Mathematical solutions find practical uses in science‚ engineering‚ and everyday problem-solving‚ contributing to advancements in technology and research‚ while also enhancing analytical thinking and logical reasoning skills.
7.1. Practical Uses in Science and Engineering
Mathematical solutions are integral to scientific and engineering advancements. They enable accurate modeling of physical phenomena‚ such as fluid dynamics and structural analysis. In mechanics‚ these solutions optimize system designs‚ while in thermodynamics‚ they predict heat transfer and energy efficiency. Engineers rely on these tools to develop innovative technologies‚ ensuring safety and performance in real-world applications across various disciplines.
7.2. Impact on Everyday Problem Solving
Mathematical solutions enhance everyday problem-solving by providing structured approaches to real-world challenges. They aid in budgeting‚ optimizing routes‚ and understanding statistical trends. By applying mathematical reasoning‚ individuals can make informed decisions‚ manage resources efficiently‚ and analyze data effectively. These skills foster critical thinking and logical reasoning‚ empowering individuals to tackle complex situations methodically in both personal and professional contexts.
7.3. Contribution to Mathematical Research
Mathematical problem solutions often contribute significantly to research by introducing novel methods or verifying existing theories. They inspire further exploration‚ advancing fields like calculus‚ algebra‚ and geometry. Breakthroughs in problem-solving can lead to new theorems or formulas‚ enriching mathematical literature. These advancements not only enhance academic understanding but also provide foundational tools for addressing future challenges in mathematics and related disciplines‚ fostering a cycle of discovery and innovation.
Mathematical problem-solving is a journey of discovery‚ blending logic and creativity. Each solution‚ whether simple or complex‚ contributes to a deeper understanding of mathematical principles and their applications.
8.1. Summary of Key Points
Mathematical problem-solving involves understanding the problem’s structure‚ applying relevant concepts‚ and verifying solutions. Resources like textbooks‚ online tutorials‚ and practice worksheets aid in mastering various math challenges. Technology‚ such as graphing calculators and AI tools‚ enhances problem-solving efficiency. Consistent practice and exploring real-world applications deepen mathematical understanding‚ fostering critical thinking and creativity in tackling complex problems effectively.
8.2. Encouragement for Further Exploration
Exploring mathematical problems fosters a deeper understanding of concepts and enhances problem-solving skills. Utilize resources like textbooks‚ online tutorials‚ and practice worksheets to refine your abilities. Embrace technology‚ such as AI tools and educational apps‚ to streamline learning. Persist in tackling challenges‚ as each problem solved brings you closer to mastering mathematics and uncovering its beauty in real-world applications and advancements.
8.3. Final Remarks on the Importance of Math
Mathematics is the cornerstone of logical reasoning and problem-solving‚ shaping advancements in science‚ engineering‚ and everyday life. Its universal language provides tools to analyze and understand complex phenomena. Embracing math fosters critical thinking and creativity‚ preparing individuals to tackle real-world challenges. Continued exploration and mastery of mathematics open doors to innovation and intellectual growth‚ emphasizing its enduring significance in shaping our world.

Additional Resources and References
Explore textbooks‚ online forums‚ and educational apps for in-depth problem-solving guides. Practice worksheets and PDF guides offer hands-on experience‚ enhancing mathematical understanding and proficiency.
9.1. Recommended Reading Materials
Textbooks like “Applied Mathematics” by J. David Logan and problem compilations by authors such as D. J. Newman offer comprehensive insights. NCERT solutions and materials from the Putnam Mathematical Competition provide structured approaches. Additionally‚ resources like “The Red Book of Mathematical Problems” and “Problem Solving Questions” include detailed explanations. These materials cover algebra‚ calculus‚ and advanced topics‚ helping students apply mathematical concepts effectively and deepen their problem-solving skills through practice.
9.2. Links to Useful Websites
Useful websites include NCERT Solutions‚ DeepMath‚ and Putnam Competition Archives. These platforms offer detailed solutions‚ practice problems‚ and study materials. Additionally‚ Math Open Reference provides interactive tools for geometry and algebra‚ while Khan Academy offers video tutorials. These resources support diverse learning styles and cater to both basic and advanced mathematical problem-solving needs‚ ensuring comprehensive understanding and skill development.
9.3. Suggested Practice Problems
Practice problems are essential for mastering mathematical concepts. Start with foundational questions from NCERT Solutions and Putnam Competition Archives. For advanced topics‚ explore problems on calculus‚ algebra‚ and number theory from DeepMath. Additionally‚ solve problems like proving sequence limits or demonstrating number properties‚ as seen in Problem Solving Questions. These exercises enhance problem-solving skills and deepen mathematical understanding effectively.
